Nordnet Robosave vs. Avanza Auto ett år senare

Tjena bloggen och folket!

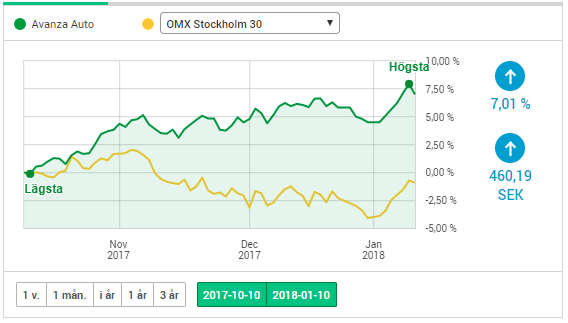
Jag kommer inte att grotta ned mig i huruvida den ena roboten är bättre än den andra men här nedan ser ni själva resultatet av min ödmjuka ettårsjämförelse.

Förutsättningarna är som nämnts exakt likadana för båda robotarna.

1. 5 000 kronor investerades som bas i vardera roboten
2. 500 kronor sattes varje månad in och vardera robot valde själv hur slantarna skulle investeras. 
3. Efter exakt ett år utvärderas resultatet.

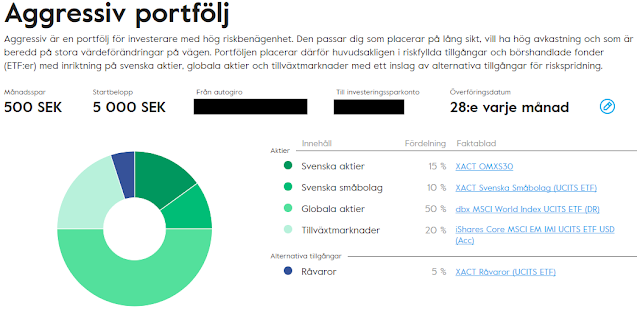
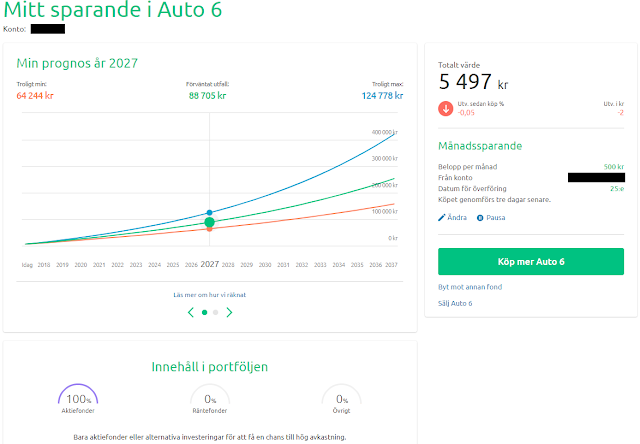
Värt att nämna är att Avanza Auto endast köper på sig av fonden Auto 6 (den mest aggressiva) varje månad medans Nordnets robot köper och säljer olika värdepapper utefter eget tycke och smak (eller i vart fall enligt fördefinierade regler).

Bilderna får tala för sig själva. Personligen så anser jag att sparrobotar likt dessa är utomordentligt bra för de personer som inte har något som helst intresse av aktier/fonder och/eller sådana som helt enkelt inte orkar bry sig. De som bara vill att saker och ting ska fungera utan att de behöver lyfta ett finger eller ens ägna skiten en tanke. Man får det man betalar för och i detta fall med endast ett 365-dagarstest som bas så visar det sig ligga någonstans i häradet 12-15% avkastning. Skulle dessa båda robotar kontinuerligt år ut och år in ligga och pusha 12+ procent så anser jag det vara en mycket god affär. Frågan är väl dock hur dessa sköter sig vid en rejäl sättning?

Har man 20+ år på sig att spara så torde det spela mindre roll vilken av de båda robotarna man väljer (eller någon av de andra robotarna på marknaden för den delen). Det viktiga är att man sparar hela tiden och så gott man kan trycker in pengar i sin pengamaskin. Gör man det så köper man ju i ur och skur och varje köp i nedgång återbetalar sig oftast rejält när det väl vänder uppåt. Jag tycker inte man skall stirra sig blind på hur ens värdepapper utvecklat sig från en vecka till en annan. De allra flesta skulle nog må bra både ekonomiskt och mentalt av att inte sitta och glo på skärmen de dagar det lyser rött över hela brädet. Det känns ju i magen när det börjar försvinna tusenlappar, tiotusingar eller rent av hundratusingar från en dag till annan.

Nå, slutklämmen måste väl ändå vara något i stil med "Gör som FAN du vill, det är dina pengar men skyll inte på mig när dina aktier i Fermenta visat sig värdelösa!" :)

Nordnet Robosave vs. Avanza Auto - sex månader

I vanlig ordning så är jag sent ute med min uppdatering av RS vs AA, riktigt sent ute denna gång men det har sina anledningar. Här kommer hur som en halvårsuppdatering av robotslaget i form av två bilder, notera även grafen för OMXS30. Om större intresse finns för hur jag gått tillväga finns så föreslår jag lektyr i form av tidigare publicerat inlägg.

När detta skrivs (13:25) den 3:e maj 2018 så är värdeutvecklingen sedan 2017-10-10 för de två enligt följande:

• Nordnet Robosave +11,21 %
• Avanza Auto +10,69 %

Nordnets robot snubblar därmed över mållinjen något hårstrå före Avanzas dito efter sex månader in action. OMXS30 har under samma tidsperiod (2017-10-10 fram till idag) inte roat sig med mycket positivt utan landar på -3,99 %. Nu borde jag väl kanske jämföra med något annat vettigare index, SIXRX månne? Någon som har synpunkter på detta? Förslag emottages tacksamt.

PS. Bilderna visar som sagt hur de två robotarna presterat fram till 2018-04-10, inte fram till dags dato. En del har ju hänt de senaste 3½ veckorna så tänk på det innan ni jämför siffrorna ovan med graferna nedan. :)

Hur stor del av din pension ger du till guds hus?

Idag gott folk, idag är en bra dag att prata om gud och guldkalven!

De allra flesta av oss har väl någon gång läst eller hört om den där guldkalven och att man inte skall dyrka mammon, ni vet det där det pratas om i den där sci-fi-boken Bibeln. Jag tänkte idag gå igenom hur mycket det faktiskt kan kosta att sponsra svenska kyrkan och att det dessutom är SJUKT dyrt att dö här i "gamla Svedala". Jag kommer att utgå från min egen situation och sedan jämföra med det dyraste stift jag hittat.

Jag betalar litet drygt 100 kr i månaden, detta år och något liknande (en troligtvis ökande summa) resten av livet i begravningsavgift till svenska kyrkan. Ponera att jag sparar dessa 103 kr varje månad i några väl valda aktiefonder som presterar ungefär 8% i årlig medelavkastning. Ponera även att jag hade jobbat från skolslut till pensionering och gissa därefter hur mycket dessa ynka 103 spänn blivit efter ett helt yrkesliv?

Svaret: 604 567 kronor! sexhundrafyratusenfemhundrasextosju riksdaler. Jag hoppas jag får ett helt j*vla mausoleum av svenska kyrkan när jag dör för jag har då bannemig betalt för det - och litet till! Jag gick dock ur svenska kyrkan för ett antal år sedan vilket rent ekonomiskt visat sig vara ett bra beslut. Nu kan ni hålla i hatten på riktigt för nu drar det iväg, rejält! Om jag INTE hade gått ur kyrkan så hade jag betalt 628 kr/månad i kyrkoavgift (inklusive begravningsavgift) vilket sålunda ger;

3 686 100 kronor! Nästan 3,7 miljoner, smaka på den du, o store ateist (eller jubla om du är religiös)!

Nu har jag självklart räknat litet trubbigt och med min nuvarande inkomst men även om jag hade räknat ut det år för år och med respektive års inkomst så hade summan ändå blivit jättestor. Ränta på ränta is the shit men jag vet inte om jag tycker det är värt att pynta herren guds tjänare flera miljoner under ett helt yrkesliv.

Som jämförelse kan vi ta en person, vi kan kalla honom Salomo, som bor i Visby stift. Visby stift är mig veterligen det stift med allra högst kyrkoavgift. Salomo hade (med motsvarande min lön och enligt räkneexemplet ovan) betalt till biskopar och präster den nätta summan 722 kr/månad vilket då ger 4 237 841 kronor alltså 4,2 miljoner.

Förresten, betalar man kyrkoskatt/begravningsavgift även som pensionär? Om så är fallet (och även om summan är lägre) blir slutsumman än mer grotesk. Då må man i så fall lägga till 15-20 års betalningar från det man går i pension till man trillar av pinnen kring 80-85.

"Jag tar en pyramid till mitt mausoleum tack..."

Här kan du själv beräkna din kyrkoavgift
Här kan du räkna ut ränta på ränta över tid

Hur mycket sponsrar du präster och biskopar med? Känns det okej att det ändå kostar skjortan att dö i sverige trots att du redan betalat hutlösa summor under din livstid? Jag tror ingen kommer i jorden idag utan att betala minst 30 000 kronor - och då för en kista i pappkartong och utan dödsrunor och gravsten. Vad får vi ens för pengarna? Varför ifrågasätter inte fler detta ofog?

Frågorna är många, vad tycker du? Kommentera gärna eller hör av dig på twitter.

Nordnet Robosave vs. Avanza Auto efter tre månader

Något försenat så smäller jag här upp en snabb uppdatering över hur min lilla test av robotrådgivarna från Nordnet och Avanza betett sig de senaste tre månaderna. Jag hade först tänkt sammanställa månad för månad men efter litet kreativt tänkande så insåg jag att det inte direkt tjänar något större syfte iom att man med fonder och robotar sparar långsiktigt. Vad är vitsen att jämföra hur en robot skött sig gentemot en annan efter bara 20 bankdagar? Inte stor kan jag tycka, särskilt inte om folk likt jag kör med den mest aggressiva inställning som de båda robotarna har. Ska man bara spara i ett år är det ju omåttligt korkat att slänga in hela slanten åt en robot där marknaden (givet den korta tidsrymden) kan hitta på nästan vad som helst.

Nåväl, vi drar inte för stora växlar på detta utan jag svänger in två bilder som saxats rakt ur de respektive bankernas sidor. Jag kan tycka att de är rätt självförklarande men för den som inte orkar räkna själv så leder Avanzas robot Auto med 1,08 procent över Nordnets Robosave. Som referens lade jag även in OMSX30 och därmed vad den generella utvecklingen hade varit om motsvarande slantar investerats i gamla Svedala och dess 30 mest omsatta bolag.

Värt att nämna kan även vara att jag valt 2017-10-10 som startdatum då Nordnet normalt sett genomför sina köp den 9:e varje månad. Jag har inte orkat sätta mig in i exakt vilken tid på dygnet som värdepappren räknas som köpta och därför sätter jag startdatum dagen efter köpet. Avanza drar å andra sidan normalt sett iväg ett köp i sin fond-i-fond (vilket Auto faktiskt är) den 1:a varje månad. På grund av att de två robotarna inte startade exakt samtidigt så anser jag den enda rättvisa jämförelsen blir om de får samma startdatum och i och med det gäller 2017-10-10.

Avslutningsvis kan jag även lägga till att när detta skrivs (23:58) den 25:e januari 2018 så är värdeutvecklingen sedan 2017-10-10 för de två enligt följande:

• Nordnet Robosave +6,79 %
• Avanza Auto +8,52 %

Det ser efter de tre första månaderna onekligen ut som att Avanzas robot prickat mer rätt än Nordnets dito. Tilläggas bör väl även att motsvarande investering i närheten av OMXS30 hade givit en negativ avkastning. Jag återkommer igen om tre månader med ett nytt inlägg om hur det har gått de två mastodonterna emellan - ja, eller mastodont och mastodont. Hmm...

Nordnet Robosave vs. Avanza Auto

Jag skrev i ett tidigare inlägg att jag ämnade starta ett sparande hos Nordnet och dess nya robottjänst Robosave. I ganska nära anslutning till Robosave lanserade Avanza sin robottjänst Auto och vad passar då bättre än att jämföra dessa två över tid?

Sagt och gjort, ett sparande upprättades i båda robotarna och även om de skiljer sig något åt när det gäller minsta startkapital och minsta månadssparpeng så har jag försökt få starten att bli så likvärdig som möjligt. Båda robotarna har fått samma startbelopp på 5 000 kronor och till det ett månadssparande på 500 kronor vardera. Jag har även försökt få dem att starta på samma dag vilket jag missade med en dag eller så men vid sammanställningen om ett år så kommer jag att kapa de första två dagarna från båda robotarna och sedan jämföra resultatet från det datumet och 365 dagar framåt. Det skall bli spännande att se vilken av robotarna som presterat bäst och därmed vilken av dem som givit mig mest vinst eller om det nu blir så - förlorat minst pengar åt mig. För närvarande tuffar ju börsen på som ett expresslok och risken kan vara att vi står inför en sättning av mindre eller större karaktär det kommande året. Skulle en sättning ske så lär de två robotarnas olika algoritmer får bekänna färg.

För att få till en så rättvis test som möjligt så har jag valt de mest aggressiva sammansättningarna som de två respektive robotarna kan erbjuda. Maximal exponering mot aktiemarknaden är det som gäller i detta fall och sålunda gav mig de båda robotarna en portfölj enligt nedan.

Tankar om detta emottages gärna i kommentarerna nedan eller på twitter: Framtidsutdelaren

Nordnet Robosave

Avanza Auto 6

Varför 147 kronor = 8 585 kronor (eller mer)...

Jag har en plan...

Låt mig förklara.

Vi har i dagsläget ett billån på sisådär 120 000 riksdaler till den makalöst osköna räntesatsen 4,9%. Det känns sisådär att behöva betala en hel del deg i onödan så vad kan man då göra åt detta? Lendo? Hah, skulle inte tro det!

Vi knatade för några veckor sedan iväg till vår snuskigt dyra storbank (SHB) och ökade på huslånet med 300 000 kr för litet kommande husrenoveringar. Då vi inte brytt oss om att pruta på räntan så kör vi med listpriset - vilket i dagsläget är 2.05% obundet 3-månader. Det ligger iofs i pipen att sparka ut SHB även om vi gladeligen äger aktier i bankfan. Det enda storbankerna duger till idag är ju som kassako för aktieägarna, som privatkund hos dem blir man fullständigt pungslagen!

Nåväl, tillbaka till ämnet. Vi kommer att rycka 120 000 kr från de upplånade 300 000 och betala av billånet per omgående. Den matematiskt bevandrade individen märker direkt att vi sänker vår ränta med 2,85%. Med den amorteringsnivå vi har legat på sedan bilen var ny så är det ganska precis fyra år tills lånet är till fullo återbetalt. Om räntan skulle ligga kvar på dagens nivå (4,9%) kommer vi efter fyra år att ha betalat inalles 12 110 kr i ränta. Samma slutsumma ränta med vårt något billigare huslån skulle landa på 5 042 kr, en differens på 7 068 kr. Jaha, och vad är det med det då?

Ponera att man ser på det som följer: Vad vi skulle ha betalat i ränta minus det vi kommer att betala ger en viss summa (enligt ovan). Denna summa delat med 48 månader (fyra år) är vad vi, i snitt, kommer att spara per månad med den billigare räntan. Vad kan man då göra med denna differens? Varför inte investera mellanskillnaden i något vettigt som (förhoppningsvis) ger minst 8% årlig avkastning? 7 068/48≈147 kr/månad.

147 "gratiskronor" sparat varje månad i 48 månader (4 år) ger 8 585 kronor, alltså 1 517 kronor i räntevinst på tidigare nämnda besparing. Det är såklart småpengar men det må ju ändå vara bättre att spara 7 068 kronor på ett billigare lån och dessutom få 1 517 kronor i bonusränta än att ha kvar billånet med mer än dubbla räntan. Smartast hade väl iofs varit att stoppa in de där 7 068 kronorna direkt utan att sprida ut det per månad i 4 år. Denna summa hade då tack vare ränta-på-ränta get 2 548 kr istället för 1 517 kr (9 616 kr totalt) - helt klart en skönare feeling. =)

Eftersom jag skriver detta 00:30 så har jag säkert räknat snett på något ställe, om så är fallet får ni gärna hälla en hink skit över mig!

Nu blir det lopplådan, go'natt!

Robosave!

Jag bestämde mig häromveckan för att starta en testportfölj hos vår kära nätbank Nordnet. De har ju som ni kanske läst om startat upp sin nya automatiserade sparrobot "Robosave". Jag tänkte köra igång direkt men se det gick inte då jag hade för många ISK, jag förstår inte riktigt vitsen med att begränsa dessa till maximalt fem stycken. Om man är som jag och vill prova på olika strategier etc. så börjar det kännas litet väl tunnsått. Nåväl, jag hade ett för tillfället tomt ISK liggandes så efter ett litet meddelande till kundtjänst så var det tomma kontot bortplockat.

Jag loggade in och sparkade liv i Robosave för att köra lös med mina tester. Första vändan fick jag en offensiv portfölj med 25% räntor i men andra gången passade det bättre då jag svarade litet annorlunda på någon av de 10-ish frågor man får svara på. Det blev så till sist en aggressiv portfölj med allra största delen i aktiebaserade ETF:er. Det är just detta som är vitsen med Robosave, allt roboten köper och säljer i är ETF:er och inget annat.

Kostnaden ligger på 0,5% per år till Nordnet och sedan en rörlig del beroende på vilka ETF:er man får i sin portfölj. Denna rörliga del ligger på 0,15-0,23% och gör sålunda att den absolut högsta avgiften blir 0,73%. Det minsta startbeloppet är 5 000 kr och med ett minsta månadssparande på 500 kr. Man kopplar ett vanligt bankkonto via autogiro till Robosave så dras den månatliga summan den 28:e varje månad, snabbt och enkelt.

Jag planerar att köra detta i ett år så får vi se hur det fungerar. Med min sedvanliga tur så kommer århundradets krasch detta år så vi (familjen) lär väl tappa alla 11 000 kronorna i slutändan, time will tell! :)

Jag ska lägga in en blänkare i kalendern för den 28:e september 2018 så jag kommer ihåg att skriva en uppdatering i bloggen om hur det gått.